前端与算法——递推与递归
前端与算法——递推与递归
# 前端与算法——递推与递归
总有人说,前端不就是渲染渲染页面吗?为什么要学算法?学习算法不是大厂面试用的吗?
这里我想说的是:只要是处在于程序开发的范畴,就一定会用到算法。
从一个页面渲染,到各种数据处理、逻辑处理、交互处理,都会涉及到或简单粗暴、或朴实无华、或花里胡哨、或晦涩难懂的算法。
本文主要讲解一些常用的算法,希望在前端开发中能有所帮助。
有写的不好的敬请提出。
后续,我会通过凑硬币的例子给大家讲解五种常用的算法(花式凑硬币 (opens new window))。
(opens new window))。
# 一、算法的基本概念
# 1、算法的特性
# (1) 输入输出
有 0 个或多个输入,一个或者多个输出。
输出可以是 return 值,也可以是对对象的改变,也可以是输出。
当然,在很多开发规范中,都会要求函数需要明确返回一个值。
# (2) 有穷性
算法的执行步骤有限,不会出现死循环,且执行时间是可以接受的。
# (3) 确定性
每一步骤含义明显,不会出现二义性。
# (4) 可行性
每一步都能通过有限次数完成。
# 2、算法设计的要求
# (1) 正确性
无语法错误,对数据能做出正确的响应。
# (2) 可读性
并不是代码越少算法就越好,需要考虑算法的维护性。
# (3) 健壮性
对非法的数据都能做出正确的响应。
# (4) 效率高,存储低
好的算法要求在执行效率和计算存储上都有要求。
# 3、算法的复杂度
通常使用 大 O 记法 来表示算法的复杂度。
# (1) 时间复杂度
Tn=O(f(n)),Tn 表示关于 n 所需要的执行次数,n 表示执行过程中的规模。
# (2) 空间复杂度
Sn=O(f(n)),Sn 表示关于 n 所占用的储存空间,n 表示执行过程中的规模。
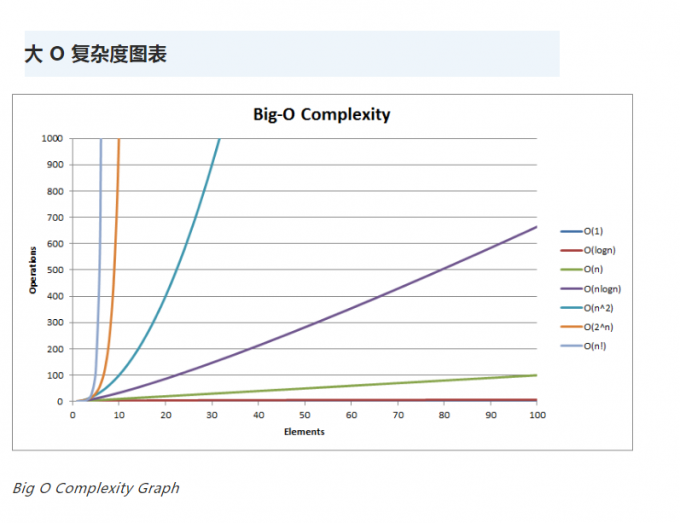
# (3) 常见的复杂度比较
在规模比较小的时候,时间复杂度消耗是相差不大的。
但是,随着规模的增长,集中算法的时间复杂度相差越来越大。
此时的算法时间复杂度排序为:
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
平时开发的过程中,可以参照上表尽可能的简化算法的复杂度。
平时在开发过程中,对于一些数据的处理,我们可能并不会过于深究效率,完全按照自己的想法来。
但是,这确实是可以进行推敲的点。
# 三、基础算法
这里我要说的是编程界最基础的算法思想:递推与递归。
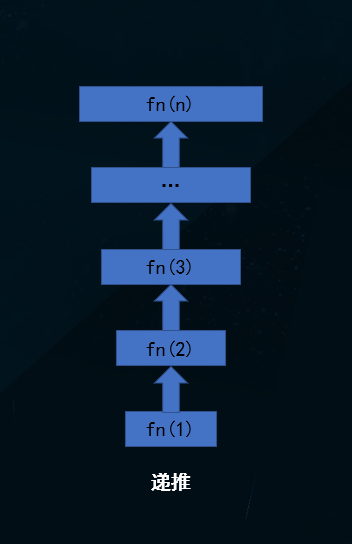
# 1、递推
基于已有条件推导下一次的结果。
例:
// 从1加到指定数字
const sum = (target) => {
let s = 0;
for (let i = 0; i < target; i++) s += i;
return s;
};
2
3
4
5
6
# 2、递归
不断的将大的问题拆解成小的问题,回归小问题的结果到大问题上,最终得出最终结果。
例:
// 从1加到指定数字
const sum = (target) => (target ? target + sum(target - 1) : 0);
2
# 3、越界代偿
用一个无害的值取代一个无意义甚至有害的值
// bad
const sum = (arr, index) => {
if (index === arr.length - 1) return arr[index];
return arr[index] + sum(arr, index + 1);
};
// good
const sum = (arr, index) => {
if (index === arr.length) return 0;
return arr[index] + sum(arr, index + 1);
};
2
3
4
5
6
7
8
9
10
11
该方法有助于快速的理解临界条件进行的处理,便于代码维护。
# 4、思想与代码实现
递推思想是可以用递归实现的,同样的递归的思想也可以用递推来实现
# (1) 递推代码实现递推思想
特点:由已知推导未知,目的明确
// 由1加到100
const sum = (target) => {
let s = 0;
for (let i = 0; i <= target; i++) s += i;
return s;
};
console.log(sum(100));
2
3
4
5
6
7
逐个计算从 1 加到 100 的过程,这个过程是很自然的
# (2) 递归代码实现递归思想
特点:自顶向下,代码简洁,自调用
// 由 1 加到 100
const sum = (target) => {
if (target === 0) return 0;
else return target + sum(target - 1);
};
console.log(sum(100));
2
3
4
5
6
将大问题逐步拆解成同类型的小问题,并使用该方法再次进行计算,直到拆解到最细粒度,最后计算出结果。
# (3) 递推代码实现递归思想
特点:自顶向下,顺理成章,自调用,避免内存溢出
// 对于任意整数n,若为奇数,则运算n=n*3+1,否则运算n=n/2,直到n为1为止,
// 计算找出1到10000中,哪个数字需要的运算次数最多?
// 使用 map 避免进行重复的计算
const map = new Map([[1, 0]]); // 初始值:当 n 为 1 时,次数为 0
// 计算某次查找需要的次数
const count: (number, total) => number = (n: number, total) => {
if (!map.has(n))
map.set(n, 1 + count(n % 2 ? n * 3 + 1 : Math.floor(n / 2), total));
return map.get(n);
};
// 查找最大次数的数字
const findMaxLen = (deepth: number, max: number, maxNum: number) => {
// 尝试使用递归,但是内存溢出了
// if (deepth === 1) return maxNum;
// else {
// const curCount = count(deepth, 0);
// if (curCount > max) {
// max = curCount;
// maxNum = deepth;
// }
// return findMaxLen(deepth - 1, max, maxNum);
// }
// 使用递推(循环)可以避免内存溢出
for (let i: number = deepth; i > 0; i--) {
const curCount = count(i, 0);
if (curCount >= max) {
max = curCount;
maxNum = i;
}
}
return maxNum;
};
console.log(findMaxLen(10000, 0, 1));
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
混合使用的情况往往是为了解决内存溢出的问题。
# (4) 递归代码实现递推思想
特点:自底向上,能简化代码
该写法比较特殊,且实用价值不高,这里不做讲解了。
# 5、前端递归的补充
# (1) JavaScript 函数的尾调用
函数调用会在内存形成一个调用帧,保存调用位置和内部变量等信息。
一个函数内存在其他函数调用,其他函数就会在这个函数上形成调用帧,所有的调用帧形成了一个调用栈。
尾调用是指在函数的最后一步操作时,返回另一个函数的调用,这个时候,由于不会用到被调用函数的位置和内部变量等信息,不需要保留外层函数的调用帧。
const fun1 = () => 10;
const fun2 = () => {
return fun1(); // 尾调用
};
const fun3 = () => {
return 1 + fun1(); // 最后一步不是函数调用,非尾调用
};
const fun4 = () => {
const val = fun1();
return val1; // 最后一步不是函数调用,非尾调用
};
const fun4 = () => {
fun1(); // 最后一步是一个隐藏的 return undefined, 不是函数调用,非尾调用
};
2
3
4
5
6
7
8
9
10
11
12
13
14
# (2) JavaScript 函数的尾递归
函数递归对内存消耗很大,每次递归都会产生一个调用帧,而整个递归下来会产生很多的调用帧,很容易出现栈溢出的问题。
尾调用是可以有效减少执行栈的,将尾调用和递归结合,有可能将复杂度为 O(n)的计算变成 O(1)。
非尾递归
function Fibonacci(n) {
if (n <= 1) return 1;
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
Fibonacci(10); // 89
Fibonacci(100); // 运行超时
Fibonacci(500); // 运行超时
2
3
4
5
6
7
尾递归
function Fibonacci2(n, ac1 = 1, ac2 = 1) {
if (n <= 1) return ac2;
return Fibonacci2(n - 1, ac2, ac1 + ac2);
}
Fibonacci2(100); // 573147844013817200000
Fibonacci2(1000); // 7.0330367711422765e+208
Fibonacci2(10000); // Infinity
2
3
4
5
6
7
注意:目前只有 safiri 与低版本的 node 支持尾递归,且 v8 默认是关闭该功能的(v8 团队认为做尾递归优化存在一系列问题,因此倾向于支持用显式的语法来实现,而非做优化),低版本 node 尾递归优化只在严格模式下生效,在执行时需加上参数 --harmony_tailcalls,node 最新版本已经移除了该功能
# (3) 蹦床函数
即便浏览器不支持,但只要围绕 尾递归的本质是减少函数调用栈 这一点,就可以做出优化,例如通过 **蹦床函数 **将递归改为循环,当然,若非必要,可以直接写循环函数,从而避免写递归函数
蹦床函数:能将递归函数转化为循环
// 蹦床函数
function trampoline(f) {
while (f && f instanceof Function) {
f = f();
}
return f;
}
2
3
4
5
6
7
# 四、常用算法
# 1、分治法
分治法是将原问题进行多次拆解,分解成了多个类似原问题的子问题,求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
因为该思想和递归最为接近,均为自顶向下,因此一般用递归的方法实现。
# 特征
分治法所能解决的问题一般具有以下几个特征:
1)、 该问题的规模缩小到一定的程度就可以容易地解决;
2)、 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
3)、 利用该问题分解出的子问题的解可以合并为该问题的解;
4)、该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
# 例子
使用 2 分、3 分、5 分的硬币凑齐 21 分,最少可以用多少硬币?
# (1) 解题思路
1> 每次选择硬币后,将问题缩小为组合剩余数额硬币的子问题
2> 在多次缩小问题后,问题缩小到剩余额度刚好等于硬币额度或者小于0,小于0意味着组合失败
3> 整理结果,得出最佳答案
# (2) 解题代码
const change = (coins, n) => {
let count = -1; // 最少次数
if (n < 0) return count; // 拼凑失败,返回-1
for (const coin of coins) {
if (n === coin) return 1; // 拼凑成功,返回1
const curCount = change(coins, n - coin);
if (curCount === -1) continue;
if (count === -1 || count > curCount + 1) count = curCount + 1; // 本拼凑数是否更少
}
return count;
};
(() => {
const coins = [2, 3, 5];
const minCount = change(coins, 21);
console.log("minCount:", minCount);
})();
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# (3) 时间复杂度
设m为硬币数,n为组合额度,由于每次的组合硬币数会小于等于n,因此设k为大于0小于1的常数,有:
T(n) = O(m * m ^ (k * n) = m ^ [(k + 1) n])。
取最小值得:T(n) = O(m ^ n)。
由于这里的硬币数为3,因此 T(n) = O(3 ^ n)。
从算法性能上来看,时间复杂度呈指数增长,凑的数额 n 越大,性能耗费会越多。
注意 3^n 增长速度十分迅速。
# (4) 算法性能
凑齐21分的运算时间: 小于1ms。
凑齐42分的运算时间: 约38ms。
凑齐63分的运算时间: 约62000ms。
凑齐630分的运算时间: 超时。
凑齐6300分的运算时间: 超时。
运行时长和算法时间复杂度预估的情况差不多。
注意:运算时间会因不同设备而异,这里的数据仅供参考与验证。
# (5) 小结
原问题为寻找能凑齐 21 分的硬币组合,被逐渐分解成,能分解成寻找更小数值的组合。
在进行组合的过程中,由于硬币的先后选择顺序不一样,会产生重复的组合结果进行运算。
但是由于问题是查找最小的硬币数,因此组合结果是可以重复。
但是我们可以确定,分治法不适合用于有重复子集的情景。
# 典型代表
二分搜索、棋盘覆盖、合并排序、最接近点对问题、循环赛日程表、汉诺塔、Fibonacci 数列、阶乘、快速排序......
# 2、动态规划
动态规划和分治法类似,也是将一个原问题分解为若干个规模较小的子问题,递归的求解这些子问题,然后合并子问题的解得到原问题的解。
# 区别
动态规划和分治法的区别在于:
分治法适用于子问题互斥的场景,而动态规划适用于子问题重叠的场景,该策略会将解存储起来,下次再次求解时直接引用。
动态规划所解决的问题是分治法所解决问题的一个子集,用动态规划来解决效率会更高。
# 关键点
动态规划的关键点在于:
- 动态规划法试图只解决每个子问题一次
- 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接取出
# 例子
使用 2 分、3 分、5 分的硬币凑齐 21 分,最少可以用多少硬币?
# (1) 解题思路
1> 每次选择硬币后,将问题缩小为组合剩余数额硬币的子问题
2> 从小到大开始运算,得出小问题的结果
3> 在单次运算完成后,若有缓存,则比较得出最佳值
4> 遍历结束,得出整体的结果
# (2) 解题代码
const change = (coins, n, cache) => {
let minCount = -1; // 最少次数
if (n < 0) return minCount; // 拼凑失败,返回-1
if (cache.has(n)) return cache.get(n); // 若存在缓存,直接取出
for (const coin of coins) {
if (n === coin) return 1; // 拼凑成功,返回1
const curCount = change(coins, n - coin, cache);
if (curCount === -1) continue;
if (minCount === -1 || minCount > curCount + 1) minCount = curCount + 1; // 本次拼凑数是否更少
}
cache.set(n, minCount); // 缓存本次执行的最小拼凑次数
return minCount;
};
(() => {
const coins = [2, 3, 5];
const cache = new Map();
const minCount = change(coins, 21, cache);
console.log("minCount:", minCount); // 5
})();
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# (3) 时间复杂度
代码上,该方法和分治法差不多,但是事实上,实际执行的代码情况其实可以转换为以下:
const change = (coins, n) => {
let max = n + 1; // 缓存数组
const dp = new Array(max);
dp.fill(max);
dp[0] = 0; // 当拼凑数额为0时,最少需要0个硬币
for (let i = 1; i <= n; ++i) { // 将会拼凑数额1的硬币到数额n的硬币
for (let j = 0; j < coins.length; ++j) { // 获取一次拼凑的最小次数
if (coins[j] <= i) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1); // 根据上一次的最小拼凑数,得到下一次的最小拼凑数
}
}
}
return dp[n] > n ? -1 : dp[n]; // 拼凑 n 的次数比 n 本身大,则说明 n 不存在最小次数
};
2
3
4
5
6
7
8
9
10
11
12
13
14
此时,可以得出时间复杂度为:T(n) = 3*n
从时间复杂度来看,运算次数会随n值增大而增大,但是增长率远远小于分治法。
# (4) 算法性能
凑齐21分的运算时间: 小于1ms。
凑齐42分的运算时间: 小于1ms。
凑齐63分的运算时间: 小于1ms。
凑齐630分的运算时间: 小于1ms。
凑齐6300分的运算时间: 约9ms。
算法的运行时长与算法时间复杂度预估差不多,消耗很少。
# (5) 小结
在采用分治法时,计算过程中产生了重复运算。导致数额大时,性能耗费的很多。
这里我们使用了动态规划,在得出组合结果后,记忆化结果,再计算时,直接跳过运算取出结果,每个问题只会计算一次。
因此,表面上,两者的时间复杂度差不多,但实际上动态规划的时间复杂度会远小于分治法。
这点微小的区别就是分治法和动态规划的区别,也明确了两种思想使用的场景。
# 典型代表
最长公共子序列、最优二叉查找树、近似串匹配问题......
# 3、分支限界法
分支界限法以广度优先搜索或者最小耗费优先的方式搜索解空间
分支定界法的基本思想是对有约束条件的最优化问题的所有可行解空间进行搜索。
在执行时,把全部可行的解空间不断分割为越来越小的分支,并为每个子集内的解的值计算一个下界或上界。
在每次分支后,对超出界限的子集不再做进一步分支,从而缩小了搜索范围。
直到这一过程找出可行解为止,该可行解的值不大于任何子集的界限。
因此这种算法一般可以求得最优解。
图示:
注: 蓝色表示某次解空间的大小,红色表示被剪枝的部分,黄色表示搜索过的部分。
可以看出遍历完成后,最后搜索的未剪枝的解空间就是最优解。
# 例子
使用 2 分、3 分、5 分的硬币凑齐 21 分,最少可以用多少硬币?
# (1) 解题思路
1> 定义一个下界值,初始为0,在第一次组合成功后赋有意义的值
2> 在每次组合的过程中,判断已经组合的硬币数是否大于等于下界值,若是,则没有必要继续往后组合,若不是,则继续组合
3> 在组合完成后,将该次组合的硬币数设置为新的下界值
4> 在所有组合完成后,此时的下界值就是答案
# (2) 解题代码
const combinationSum = function (coins: number[], target: number) {
// 最小硬币数
let min = 0;
// coins.sort((a, b) => b - a); // 从大到小排序
const length = coins.length;
const comb = (start: number, sum: number, count: number) => {
if (min && count >= min) return;
if (sum >= target) {
if (!min) min = count;
if (sum === target) min = count < min ? count : min;
return;
}
count++;
for (let index: number = start; index < length; index++) {
const combItem: number = coins[index];
const nextSum: number = sum + combItem;
if (nextSum <= target) comb(index, nextSum, count);
}
};
comb(0, 0, 0);
return min;
};
console.log(combinationSum([2, 3, 5], 21));
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# (3) 时间复杂度
从表面上看,时间复杂度 Tn = O(3 ^ (k * n));
但由于该思想会不断的进行组合,并求出下界值,大于下界值的运算会被直接舍弃,因此并不能简单这么算。
设k为设k为大于0小于1的常数,平均组合次数为 k*n,则该运算可以转换为以下代码:
let count = [2, 3, 5, ... , 3, 2]; // 数组长度为 k*n
let sums = [];
for (let i = 0; i < k*n; i++) sums[i] = count.reduce((sum, item) => sum + item, 0); // 注意数组为抽象的数组
2
3
此时,我们可以得出其时间复杂度为:
T(n) = O((k*n) ^ 2 = k^2 * n^2)
当硬币数组从大到小排序时,k最小,T(n)有最小值,当硬币数组从小到大排序时,k最大,T(n)有最大值。
# (4) 算法性能
从小到大:
注意,我们的例子中,硬币的排序默认是从小到大的。
也就意味着,时间复杂度会处在最大值的水平。
因此,运算时间是处于最大值的水平。
凑齐21分的运算时间: 约2ms。
凑齐42分的运算时间: 小于1ms。
凑齐63分的运算时间: 约1ms。
凑齐630分的运算时间: 约15ms。
凑齐6300分的运算时间: 约11400ms。
从大到小:
而后,我们放开上面的从大到小排序注释,再次进行统计。
此时,时间复杂度会处在最小值的水平。
因此,运算时间是处于最小值的水平。
凑齐21分的运算时间: 约2ms。
凑齐42分的运算时间: 小于1ms。
凑齐63分的运算时间: 小于1ms。
凑齐630分的运算时间: 约9ms。
凑齐6300分的运算时间: 约5200ms。
乱序:
若是乱序,该方法的真实性能会处于上述的两个时间之间。
一般的,我们可以采取排序后再运算,这样可以剪去较多的枝。
当然,排序其实也是参杂了一点贪心算法的思想在里面了。
但是,贪心算法和分支限界是有本质区别的,后续我们会继续讲到贪心算法。
# (5) 小结
这次,我们使用了一个界限值,这个界限值在第一次组合成功后会进行记录。
后续运算若超出界限值,则直接中断搜索;若小于界限,则再次记录。
而在不停的遍历中,就能找到最小的那个界限值,这个界限值也就是问题的答案了。
这种思想称之为分支限界法。
# 典型代表
任务分配问题、多段图的最短路径问题、批处理作业调度问题、电路布线问题......
# 4、贪心算法
在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
# 基本思路
建立数学模型来描述问题。
把求解的问题分成若干个子问题。
对每一子问题求解,得到子问题的局部最优解。
把子问题的解局部最优解合成原来解问题的一个解。
# 例子
使用 2 分、3 分、5 分的硬币凑齐 21 分,有哪些组合?
# (1) 解题思路
1> 首先将硬币从大到小排序
2> 每次取硬币的最大额度值,并计算已组合的额度值
3> 若已组合的额度大于要凑的额度,则组合失败,前一次取的硬币额度值往后一位取(由于排序,取的值会比前次的小一点)
4> 若已组合的额度小于要凑的额度,则继续取值
5> 若已组合的额度刚好等于要凑的额度,则完成组合
# (2) 解题代码
const combinationSum = function (coins: number[], target: number) {
let min = 0;
// 硬币从大到小排序
coins.sort((a, b) => b - a);
const length = coins.length;
const comb = (start: number, sum: number, count: number) => {
if (min) return;
if (sum >= target) {
if (!min) min = count;
if (sum === target) min = count < min ? count : min;
return;
}
count++;
for (let index: number = start; index < length; index++) {
const combItem: number = coins[index];
const nextSum: number = sum + combItem;
if (nextSum <= target) comb(index, nextSum, count);
}
};
comb(0, 0, 0);
return min;
};
console.log(combinationSum([2, 3, 5], 21));
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# (3) 时间复杂度
由于该思想会不断的查找最大值进行组合,从而实现最小化运算量的目的。
代码层面上,该算法的时间复杂度Tn = O(3^n)。
设硬币数为c, 设每次组合时,某次能循环的系数为:k1, k2, k3...kn,当kjn-1为1时,kjn及其后的值均为0,kjn之前的值均为1。
设 j 为大于0小于1的常数,平均组合硬币数为 j*n,则有:
Tn = (k1 + (1-k1)*c) * (k2 + (1-k2)*c) * ... * (kjn + (1-kjn)*c)
Tn = k1*k2*...kjn + (k1*k2 * ... * kjn-1 * c^(kjn)) ... +c^(1+jn)
1> 最大值
当kjn为1时,kjn之前的值均为1。
因此我们可以得到最大值 Tnmax = (k1*k2*...kjn-1)c + ... + c^jn。
去除低阶项,去除常数项,代入硬币数,得 Tnmax = 3^n。
这种情况意味着什么呢?当整个硬币数组所有的组合均不能组合成组合额度时,此时的消耗为很大。
2> 最小值
当k1为1时,k2及其后的值均为0。
因此我们可以得到最小值 Tnmin = k1*(1-k1)*c+k1*(1-k2)*c+kn*(1-kn)*c = j * n * c
去除常数项,得 Tnmin = n
这种情况意味着什么呢?当整个硬币数能被组合额度整除时,其运算会最高效。
3> 中间值
一般来说,我们使用贪心算法,是在能有解,且适合多次取最佳值的的场景,因此,一般的时间复杂度会比最小值稍微高一点。
设需要再次寻找较大值的消耗系数为 z (0 < z < 1),此时的需要的消耗值为 z * n。
时间复杂度为:Tn = (z + 1) * n
# 4) 算法性能
凑齐21分的运算时间: 约2ms。
凑齐42分的运算时间: 小于1ms。
凑齐63分的运算时间: 小于1ms。
凑齐630分的运算时间: 约1ms。
凑齐6300分的运算时间: 小于1ms。
由于贪心策略每次都是取的最大值或较大值,避免了大量的计算,因此性能表现极佳。
运算的消耗较少,与时间复杂度的预估情况一致。
# (5) 小结
贪心算法80%的代码和分支限界法相似。
但是,分支限界法的最佳运算结果,在组合凑6300分时,任然与贪心算法运算差距巨大,为什么?
分支限界法,是广度优先的算法,确实,第一次组合的值是最佳值,但是它会全部遍历。
但是该方法并不知道第一次是最佳值,它会继续组合到遍历结束,组合过程中,若次数超过最佳值后就会中止继续组合。
而这里,我们将问题转换成了,每次选择最大值的做法,这样我们减少了大量的无效运算,且所得到的次数是最少的。
# 典型代表
最近邻点问题、最短链接问题、图着色、背包问题、多极度调度问题、霍夫曼编码、单源最短路径、最小生成树......
# 5、回溯法
回溯法是一种搜索算法,从根节点出发,按照深度优先搜索的策略进行搜索,到达某一节点后 ,探索该节点是否包含该问题的解,如果包含则进入下一个节点进行搜索,若是不包含则回溯到父节点选择其他支路进行搜索。
# 设计步骤
回溯法的设计步骤如下:
1)针对所给的原问题,定义问题的解空间
2)确定易于搜索的解空间结构
3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数除去无效搜索
# 例子
使用 2 分、3 分、5 分的硬币凑齐 21 分,有哪些组合?
# (1) 解题思路
1> 为了剪枝(减少重复运算),先将硬币数组从小到大排序,通过控制内部遍历的起始点避免重复运算
2> 通过双重遍历获取所有的组合
3> 在单次组合完成后,向上层回溯,继续组合
# (2) 解题代码
const combinationSum = function (coins: number[], target: number) {
// 硬币从小到大排序
coins.sort((a, b) => a - b);
const results: number[][] = new Array<number[]>();
const length = coins.length;
const comb = (start: number, sum: number, arr: number[]) => {
if (sum >= target) return sum === target ? results.push(arr) : void 0;
for (let index: number = start; index < length; index++) {
const combItem: number = coins[index];
const nextSum: number = sum + combItem;
if (nextSum <= target) comb(index, nextSum, arr.concat(combItem));
}
};
comb(0, 0, []);
return results;
};
console.log(combinationSum([2, 3, 5], 21));
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# (3) 时间复杂度
这里采取了完全遍历,我们设k为大于0小于1的常数,平均组合硬币数为 k * n,硬币数组长度为m。
此时,算法的时间复杂度T(n) = O(3 ^ (k * n))。
# (4) 算法性能
组合21分的运算时间: 小于1ms
组合42分的运算时间: 小于1ms
组合63分的运算时间: 约1ms
组合630分的运算时间: 约1890ms
组合6300分的运算时间: 超时
因为算法的时间复杂度均较大,计算时间呈指数增长,且是计算所有组合路径,虽有除去重复计算,但计算量还是挺大,消耗性能多。
# (5) 小结
还是这个硬币组合问题,这次我们是查找所有组合。
此时的解空间为所有等于目标正整数的数字组合。
由于数字可以重复选择,解空间结构为给定数组的最小元素到最大元素之间的所有无重组合。
因此在这里会存在一个双重遍历,在遍历过程中,为了避免重复组合,第二层遍历会取第一层遍历的开始值,实现剪枝。
最后所有符合条件的组合均会被收集,找到问题的许多解。
这样的思路,称之为回溯法。
# 典型代表
哈密顿回路问题、八皇后问题、批处理作业调度......
# 五、引用场景
1、前端需要写逻辑的应用(如:应用了sqlite的混合应用)
2、Node中间层开发
3、ssr渲染、全栈开发
4、其他
# 结束语
本文开始讲解了一些算法相关的基础概念,再讲解了最基础的递推与递归,之后再延申到一些常用的算法,通过凑硬币理解五种常用算法的思想。
其实,每一个程序员都会对算法充满激情。
当前现状是算法对于后端来说,会用的相对比较多些,而前端用的相对少些。
这也就造成了很多前端都觉得算法与我无关、有逻辑交给后端的看法。
事实上,是否要前端用算法、是否要把逻辑给到后端,还是要根据具体情况来的。
程序有设计模式,而算法也有设计模式。上述的五种常用算法其实就是算法的设计模式。
程序的设计模式都是为了更好的开发维护,算法的设计模式是为了更好的解决问题。
至此,本文就结束了,谢谢~
# 参考文献
1、程杰. 大话数据结构. 北京:清华大学出版社:2011.6
2、刘铁猛. 算法之禅:递推与递归. 北京:中国水利水电出版社:2020.10
3、木叶秋声. 五大常用算法 (opens new window). 简书:2018.5